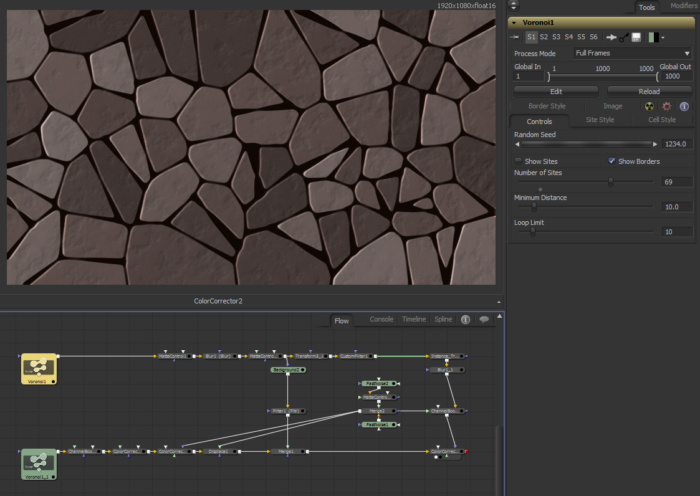
In my efforts to expand my capabilities in Fusion, and in visual effects generally, I have taken my first steps into the creation of Fuses. A Fuse is a custom tool for Fusion written in Lua. It’s sort of a half-way point between Macro and Plug-in. It’s more flexible than a Macro because it doesn’t rely on existing tools—so the Spline View won’t be cluttered by a hundred LUT controllers from Custom Tools. Unlike a Plug-in, it doesn’t require compiling, and it will run in the free version of Fusion 8.
This particular Fuse creates a Voronoi segmentation:
Before I begin, let me excuse any misinformation and bad practices in this article by saying that I have little formal training in programming. I did have some computer science classes the first time I attempted college many years ago, but only a little bit of that knowledge “stuck.” With that said, if a “real” programmer comes through here and has suggestions, I’m all ears!
The Fuse comes in two parts: The first randomly distributes a number of “Sites”—single points in the image that serve as controllers for where the lines are drawn. The second draws the lines themselves, dividing the image into “Cells.”
Creating a list of random points is fairly easy, but true randomness tends to create clumps where the points are very close together, resulting in huge variations in cell size. Since many applications of the Voronoi diagram require more evenly-distributed sites, I will use an algorithm called a Poisson process to reduce the randomness.
The usual results in a search for Poisson process or distribution are unfortunately too technical for me—I can’t even read the notation most of the time. For this Fuse, I am instead relying on the description provided by Khan Academy’s Pixar in a Box. Although the tone of those lessons seems to be aimed at students around 5th grade, I find the sophistication level of the math involved to be just about right for me. I have no idea if the method they demonstrate is efficient (probably not), but it’s at least something I can wrap my head around. If you understand the Pythagorean Theorem, you should be able to understand what I’m going to do here, although the code itself will require at least a rudimentary understanding of some programming language.
The algorithm I came up with based on watching those Khan Academy lessons is as follows:
- Ask the user for the number of points desired in the image.
- Ask the user for a minimum distance between points.
- Ask the user for the size of each point.
- Using a random number generator, generate an x,y coordinate pair.
- Using the Pythagorean Theorem, calculate the distance between this point and each previously-generated point.
- If any such distance is less than the minimum radius, discard the point and try again. Otherwise, place the point in a list.
- Continue generating new points until either the desired number is reached or the loop has run a certain number of times (prevents an infinite loop condition if there is nowhere to put a new point).
- For each pixel, determine the distance to the nearest generated point. If that distance is less than the desired point size, color the pixel white.
When I create a tool or write a program, I like to start by listing the inputs and outputs I will eventually need. I can get that information by looking at my algorithm: My inputs will be Number of points, minimum Distance, Size of point, and random Seed. Since I know my output will be an image, and the entire algorithm is based on counting pixels, I’ll also need controls for the Width and Height of the image, and also the color Depth.
Fuse Structure
Since getting the Poisson process right is a prerequisite for the Voronoi diagram, I started by creating a Fuse where I could develop just that. When I start adding more features, like animated points, I can do that development in this simpler and faster Fuse instead of trying to work in the fully developed Voronoi Fuse.
A Fuse has a few standard qualities that should be set up from the start and are frequently the same for every Fuse. First, there is a code block that the Fuse uses to report its own name and attributes to Fusion on program load. That looks like this:
FuRegisterClass("MT_Poisson", CT_SourceTool, {
REGS_Category = "Fuses,"
REGS_Name = "MT_Poisson",
REGS_OpIconString = "ppd",
REGS_OpDescription = "Poisson Point Distribution",
REG_Source_GlobalCtrls = true,
REG_Source_SizeCtrls = true,
REG_Source_AspectCtrls = true,
REG_Source_DepthCtrls = true,
})
The first line is a container that describes what’s coming. It gives the name that will be used internally by Fusion: “MT_Poisson”, and the type of tool: CT_SourceTool. A SourceTool is one that creates an image. Other Class Types are CT_Tool, CT_ParticleTool, CT_Modifier, and CT_ViewLUTPlugin.
The four lines that follow, inside the curly brace, tell Fusion which tool category to place the fuse in, what name to display in the Flow View, the short-code that can be used to find the tool using Alt-Space, and a user friendly description of the tool. I don’t honestly know where that description shows up, and it’s optional, but I usually put it in anyway.
The last four lines, still inside the curly brace, set up some standard controls. They’re a quick way to get the Image and Common controls tabs without having to set up all those controls by hand. There are quite a few other attributes you can give the Fuse in this section, such as a link to a web page for documentation and authorship information, flags to turn off some of the standard controls. I learned most of this from the Fuses documentation in the VFXPedia. The information there is incomplete, and it’s not well organized in places, but there’s enough there to get you started.
The next bit of code tells Fusion what inputs and outputs the node will display in the Flow view. I’ll just give a little bit of this here. The rest of the controls I listed above will get similar blocks. If you want to look at the full code, here it is.
function Create()
InSiteNumber = self:AddInput("Number of Sites", "SiteNumber", {
LINKID_DataType = "Number",
INPID_InputControl = "SliderControl",
INP_MinAllowed = 0,
INP_MaxScale = 100.0,
INP_Default = 15.0,
INP_Integer = true,
})
end
A function is a sort of mini-program that can be included in a larger program so that you don’t have to re-write code that you use frequently. This particular function is a special case, though; it won’t be called for by the Fuse itself but by Fusion when it’s time to put the node in the Flow.
Some functions are created inside the program you are writing, but others are part of libraries that are external to your program. The Lua libraries included with Fusion contain quite a few functions that are designed specifically to be used in Fusion and that will be common to all Fusion installations. We’ll see a few of them as we go through this. Again, most of them are documented in the VFXPedia, and others, like the math functions, are part of standard Lua libraries.
Let’s walk through what we’re doing with the Create() function.
InSiteNumber is a variable that will contain information about the control I’m adding. I will use it later to send information from the Fuse’s control panel into the main program. It is assigned the output of another function, AddInput(), which is applied to a special object called “self”, meaning the tool that is being created. The AddInput function takes three arguments (information given to a function before it runs): A human-readable description, which shows up in the tool’s control panel; a scripting name, which can be addressed by expressions; and a list of attributes that the new control will have.
The control’s attributes are contained within the curly braces: { }. These braces indicate that the items between them are a table (an array in some programming languages, or a tuple in Python). The attributes that need to be defined vary based on the control type, the job it needs to perform, and how it will be displayed in the control panel. The first such attribute tells Fusion what kind of data the control will output. Almost all controls output numeric data, so the majority of controls have the line LINKID_DataType = “Number”,. Other common DataTypes are “Point”, which is a two-dimensional numerical value (a 1×2 matrix or a coordinate pair, however you want to think about it), “Image”, and “Text”.
The next line determines how the control appears in the panel. A SliderControl is the most common type of Fusion control. It usually requires you to specify its minimum, maximum, and default values, which is what the following three lines do. Finally, the last line tells Fusion that the control will output only Integer values—no decimals. This control will be used to tell the tool how many Sites it is to generate. Fractional values wouldn’t make sense, so it’s best to limit it to integers. The User Controls document at VFXPedia has documentation on all of the available controls. It’s in the Macros documentation, but most of the syntax is the same for Fuses.
All of the other controls are built in the same fashion. Once they’ve all been defined, “end” closes the Create() function. Next we move on to the Process() function, which is where the actual program lives:
function Process(req) <lots of code, described below> OutImage:set(req,out) end
The Process() function takes an argument “req”, which means Request, and it contains information about the Fusion environment, such as version number, value of each input, current frame number, and so forth. Just like the Create() function, Process() is terminated by “end”. The OutImage object gets its attributes set by the set() function, which passes the Request and the pixels that the code generates. “Out” is just the name of a variable that will contain the image.
As before, more specific information about the Process function can be found at the VFXPedia.
Importing Data from Fusion
While it is possible to build a custom Graphical User Interface (GUI) with a Fuse, it is far easier for both the user and the programmer to use a standard Fusion control panel to get user input. We’ve used the Create() function to set up the control panel, but we still need a way to connect the inputs there to variables we can use in the Fuse. For that, we use the GetValue() function. We can create a variable and assign it a value all in one line, like so:
local siteNumber = InSiteNumber:GetValue(req).Value
There are two kinds of variable in most programming languages: Local and global. A local variable is visible only inside the function where it was created. A global variable can be seen by any function in the program, and occasionally even by functions outside the program. For instance, if you have multiple copies of a Fuse in your comp, they will all have access to each other’s global variables, which can create unpredictable results. Thus, it’s usually a good idea to declare local variables unless you have no other choice.
“siteNumber” is the name of the variable. Whenever I use that word from now on, the Fuse will interpret it as meaning whatever value has been assigned to it. “InSiteNumber” was the variable name from the Create() function. I am not sure if this is a global variable or not—I tend to think that it’s contained in that Request object, but I am not sure. In any case, it is the object upon which the GetValue() function is acting. We saw that same structure up above when adding inputs to the Self object. Lua uses this syntax to apply a method to an object:
Object:Method(Arguments)
An Object is a “thing” that exists in the program. It can be a variable, or a table, a comp, or even all of Fusion. Objects can have values and attributes, which can have their own values and can be addressed as Objects themselves. We assigned several attributes to InSiteNumber when we created it, and if we needed to, we could access those attributes by name. For instance, InSiteNumber.LINKID_DataType holds the value “Number”. The . indicates that we’re looking for a sub-Object contained inside a bigger Object.
A Method is a function that is associated with a type of Object. I don’t want to get into programming theory here, so I’m going to leave it at that. In this case, the Method GetValue() retrieves the Value set by the user in the Control Panel, which is passed from Fusion to the Fuse in the Request. This convoluted interface between Fusion and the Fuse is a little hard to understand at first, but after you’ve written and debugged a few Fuses, you’ll start to understand what’s going on. It is really unnecessary to understand all of it—90% of programming is just copying other people’s code, anyway (within the strictures of the law and appropriate licenses, of course).
Each variable I will need in my algorithm will be retrieved in the same manner.
Let’s Get This Thing Moving, Already!
At this point, the Fuse can exist in Fusion, and all of the inputs are available as variables. We also have a line that will export the results of what we do here back to Fusion as an image. Finally, we can start transforming the algorithm described above into actual code. I like to copy my pseudocode into the program as comments. This not only helps to keep me on task, it also automatically documents my code as I go along. Documenting the code makes it easier to remember how the program works when I come back to it later, and it helps other coders to understand it. So here’s what I start with:
-
-- Ask the user for the number of points desired in the image. -- Ask the user for a minimum distance between points. -- Ask the user for the size of each point. -- Using a random number generator, generate an x,y coordinate pair. -- Using the Pythagorean Theorem, calculate the distance between this -- point and each previously-generated point. -- If any such distance is less than the minimum radius, discard the -- point and try again. Otherwise, place the point in a list. -- Continue generating new points until either the desired number is -- reached or the loop has run a certain number of times (prevents -- an infinite loop condition if there is nowhere to put a new point). -- For each pixel, determine the distance to the nearest generated point. -- If that distance is less than the desired point size, color the -- pixel white.
Those first three lines are taken care of by the variable assignment, so they’ll stay up there with that section of code. I’ll break out each of the next steps in turn, show some of the code, and then explain it.
Random Numbers
-- Using a random number generator, generate an x,y coordinate pair. -- Initialize random number generator math.randomseed(seed) math.random(); math.random(); math.random() -- clears out the first couple of non-random results local random = math.random -- faster in a local -- Some generic counter variables for loops local count = 0 local i = 0 -- Create list of sites -- For future versions of the tool, we want to execute this routine only once. -- if Poisson = FALSE -- While i < SiteNumber -- Assign a random location to each Site and store it in the table. -- i = i + 1 -- XLoc = rand(0,Width) -- YLoc = rand(0,Height) -- sites[i].x = XLoc -- sites[i].y = YLoc
We don’t want truly random numbers in a program like this. We want the Fuse to produce repeatable results so that it always does the same thing unless we tell it not to. A random numbers algorithm can therefore take a seed value, which tells the algorithm where to start. Every series of numbers generated from the same seed will be the same. That ensures that if we render the Voronoi on a render farm, each frame we get back will have the same pattern. The Random Seed is one of the variables we get from the control panel, allowing the user to ask for a new pattern of dots at any time.
Various sources that talk about random number generation say that the first two or three numbers a generator spits out aren’t sufficiently random, so I ask this one to spit out three right off the bat, getting them out of the way. In addition, several existing Fuses claim that the random number generator is faster if the function is assigned to a local variable. I presume that’s because the function code itself is imported into the program, and it doesn’t have to search a library for it every time it needs to be run. Now that I talk that out, I suppose I should make that assignment first, and then clear out the first three numbers.
As you can see, in addition to the pseudocode’s broad strokes, as I implement each step of the algorithm, I try to put in more comments to explain what I’m doing. Sometimes I get stuck on the actual implementation of a step, and I’ll just leave the comments to remind myself of what I need to do while I move on to something else, hoping that by the time I come back I’ll have made some kind of breakthrough. I also leave notes about things I’d like to do in the future if I make a new version. Hopefully this well-commented code will help you to better understand the Fuse and guide you in making your own or modifying this one.
Creating the list of Sites
I originally designed the code to run in two modes: a random distribution and the Poisson distribution. I eventually realized that I could get the random mode by simply reducing the Poisson disc size to 0, and I commented out this section of code. Even so, it shows the basics of how to generate an array of random locations.
-- Using the Pythagorean Theorem, calculate the distance between this
-- point and each previously-generated point.
-- If any such distance is less than the minimum radius, discard the
-- point and try again. Otherwise, place the point in a list.
-- Continue generating new points until either the desired number is
-- reached or the loop has run a certain number of times (prevents
-- an infinite loop condition if there is nowhere to put a new point).
if Poisson == TRUE
while i < siteNumber do
-- Prevents the loop from continuing infinitely if there is not
-- enough room for all the sites at the specified disc size
if count > loopLimit then break
end
-- Set a flag indicating that the current site may be written to the
-- table
approved = 1
i = i + 1
-- Assign a random location for site i
XLoc = random(0,Width)
YLoc = random(0,Height)
for j in pairs(sitesx) do
-- Compare the location of the site to that of each existing site.
-- If it is too close to any existing site, reset counter i and
-- try again
if sitesx[j] then
-- test for existence of the index
distance = math.sqrt((XLoc - sitesx[j])^2+(YLoc - sitesy[j])^2)
if distance < discSize then
i = i - 1
count = count + 1
approved = 0
break
end
end
end -- end of for
-- If the site passed all the tests, write its values to the table
if approved == 1 then
sitesx[i] = XLoc
sitesy[i] = YLoc
-- reset the loop limit counter
count = 0
end
end -- end of while
end -- end of if
Again, there’s an if statement testing for a switch that I didn’t implement. It’s hard-coded to Poisson = 1. This while is the same logic as the previous one, except that I anticipated a situation where either discSize or siteNumber or both were so large that it would be impossible to find a suitable location for all the points. So if the loop runs too many times without finding a new location, the count variable will cause it to break and continue.
As before, a random location is created, but this time it is tested against every previously generated location to see if it’s within a circle with radius discSize. That’s where Pythagoras comes in: The distance between any two points can be found using the Distance Formula. The for loop cycles through each position previously recorded in the sitesx table, making comparisons to the point currently under consideration. If it doesn’t find any point that is too close, the new point is added to the table, and the count variable is reset.
That for loop looks a little different from the kind you’d encounter in C or Python. pairs() is a special Lua function that iterates over a table. A little more information about pairs() and ipairs() is in the Lua documentation, although I highly recommend getting a copy of the book Programming in Lua for a more thorough description of the language.
Eventually, i will be bigger than SiteNumber or count will be bigger than loopLimit, and the while loop will end. At that point, there will be two tables, sitesx and sitesy, that contain x- and y-coordinates for each site. I am fairly sure that it would be better to store the coordinates as an ordered pair in a two-column table (three column? I suppose the table has an index field as well), but I was unsure of the syntax, so I did it the “wrong” way by making two tables. As long as I remember not to manipulate them separately, they should remain in sync. I know that’s going to bite me eventually if I keep doing it, though!
Making the Image
The next step is to render those points into an image.
-- Testing each pixel in the image, color it white if it is close enough
-- to a generated location.
out:MultiProcessPixels(nil, {
Sitesx = sitesx,
Sitesy = sitesy,
NodeSize = nodeSize
}, 0,0, img.Width, img.Height, img, function(x,y,p)
smallest = 200000 -- arbitrarily large number. This may break if the
-- image is more than 100k in width.
for i in pairs(Sitesx) do
if Sitesx[i] then
-- Check distance of each pixel to each site. Any pixel that is close
-- to a site node is white, with a falloff based on the nodeSize
distance = math.sqrt((x - Sitesx[i])^2 + (y - Sitesy[i])^2)
if distance < NodeSize then -- provide an option to turn this off
p.R = 1 - distance/NodeSize
p.G = 1 - distance/NodeSize
p.B = 1 - distance/NodeSize
break
end -- end of if
end -- end of if
end -- end of for
return p
end
) -- end of MultiProcessPixels
In this segment of the code, we see the MultiProcessPixels (MPP) method that can be applied to any image object. MPP is a multi-threaded process—it can act on several pixels simultaneously. This makes it much faster than a linear algorithm that must act on the pixels one-at-a-time. The method requires a few pieces of information to run: An initialization function (can be omitted by using the word “nil,” as I have done above), a table containing any variables you need it to use, the beginning and ending x- and y-coordinates for processing (the locations of the lower-left and upper-right corners of the screen area you want to affect), the image you want to process, and a function declaration that will ask for information about the specific pixel to be processed.
The variables fed to MPP must be global in scope so that all of the instances of the process can access them at once. They are therefore redeclared during the construction of the MPP call. Convention seems to be to give the global variables a capitalized version of the local variable names. Lua is case-sensitive, so Red is a different container than red. Thus, Sitesx = sitesx makes sense, and means “create a global variable called ‘Sitesx’ containing the value(s) currently assigned to ‘sitesx’.” Since sitesx and sitesy are tables, Sitesx and Sitesy also become tables when the assignment is made. Obviously, since we want to create the entire output image, the lower-left corner is at 0,0, and the upper-right is at a coordinate equal to the image’s width and height. Finally, the function declaration says that we’re going to request variables x and y, which are the current coordinate of the pixel to be acted upon, and p, which contains the color information in that pixel.
Once we get down into the method itself, we’re dealing with only a single pixel at a time. We have that pixel’s location in x and y, and we have the locations of all of the generated sites in Sitesx and Sitesy. We can therefore use the same distance formula to test whether or not our current pixel is close enough to one of those locations to be colored in. We loop through each site using pairs(), just like we did before. This time, though, if distance is ever smaller than NodeSize, we set the pixel’s color and break the loop. Rather than simply making the pixel while, I gave it a fall-off by inverting the ratio of distance to NodeSize.
Finally, return p sends the new color back out to be applied to the image the MPP method was invoked upon.
Extending the Poisson Fuse to a Voronoi Segmentation
When I began this process, I had expected the Voronoi pattern itself to be the difficult part. A Poisson distribution was something that I had a pretty good grasp of mathematically, so it seemed easy, as indeed it was. What surprised me, though, was that I had actually already done almost all of the work I needed for the Voronoi.
The lines in a Voronoi diagram are located in places that are equidistant between the two nearest points. I already had code that finds the distance to the nearest point. All I needed was to extend it to find the second-to-nearest, find out if those two distances are similar to one another, and, if they are, to apply the same coloring method as I had already developed in order to make the lines. At the same time, for any point that failed that test, I knew which cell it belonged to, so I could color all the pixels in the same cell with the same color.
I added a routine to obtain a color for each cell, each border, and each site:
-- Assign a color to each cell, each border region, each intersection, and each site node
cellColorRList = {}
cellColorGList = {}
cellColorBList = {}
cellColorAList = {}
borderColorRList = {}
borderColorGList = {}
borderColorBList = {}
borderColorAList = {}
siteColorRList = {}
siteColorGList = {}
siteColorBList = {}
siteColorAList = {}
siteSizeList = {}
for i in pairs(sitesx) do
siteColorRList[i] = ((random() * (siteRedHigh-siteRedLow)) + siteRedLow) + siteColorR
siteColorGList[i] = ((random() * (siteGreenHigh-siteGreenLow)) + siteGreenLow) + siteColorG
siteColorBList[i] = ((random() * (siteBlueHigh-siteBlueLow)) + siteBlueLow) + siteColorB
siteColorAList[i] = ((random() * (siteAlphaHigh-siteAlphaLow)) + siteAlphaLow) + siteColorA
cellColorRList[i] = ((random() * (cellRedHigh-cellRedLow)) + cellRedLow) + cellColorR
cellColorGList[i] = ((random() * (cellGreenHigh-cellGreenLow)) + cellGreenLow) + cellColorG
cellColorBList[i] = ((random() * (cellBlueHigh-cellBlueLow)) + cellBlueLow) + cellColorB
cellColorAList[i] = ((random() * (cellAlphaHigh-cellAlphaLow)) + cellAlphaLow) + cellColorA
borderColorRList[i] = ((random() * (borderRedHigh-borderRedLow)) + borderRedLow) + borderColorR
borderColorGList[i] = ((random() * (borderGreenHigh-borderGreenLow)) + borderGreenLow) + borderColorG
borderColorBList[i] = ((random() * (borderBlueHigh-borderBlueLow)) + borderBlueLow) + borderColorB
borderColorAList[i] = ((random() * (borderAlphaHigh-borderAlphaLow)) + borderAlphaLow) + borderColorA
siteSizeList[i] = (random() * siteSizeVariance) + siteSize
end
Although those are long statements, the logic is fairly simple. There’s a table to hold each color component (again, I really should find a way to store all of this linked data in a single table entry). For each entry in the sitesx table, each of those color tables gets a random number between the user-chosen minimum and maximum values. The difference between the high and low values provides the size of the range, multiplying by a random number between 0 and 1 selects a value within that range, and adding the low value shifts the range back up above or equal to the minimum.
All of these lists are fed into MultiProcessPixels along with the list of sites and a few other variables, like the border width.
-- Testing each pixel in the image, assign the appropriate color based on which region it is in
deviation = borderWidth
out:MultiProcessPixels(nil, {
Sitesx = sitesx,
Sitesy = sitesy,
SiteSizeList = siteSizeList,
Deviation = deviation,
NumSites = siteNumber,
ShowSites = showSites,
ShowBorders = showBorders,
SiteColorRList = siteColorRList,
SiteColorGList = siteColorGList,
SiteColorBList = siteColorBList,
SiteColorAList = siteColorAList,
CellColorRList = cellColorRList,
CellColorGList = cellColorGList,
CellColorBList = cellColorBList,
CellColorAList = cellColorAList,
BorderColorRList = borderColorRList,
BorderColorGList = borderColorGList,
BorderColorBList = borderColorBList,
BorderColorAList = borderColorAList
},
0,0, img.Width, img.Height, img, function(x,y,p)
smallest = 200000 -- arbitrarily large number. This may break if the image is more than 100k in width.
for i in pairs(Sitesx) do
if Sitesx[i] then
-- Check distance of pixel to site under consideration
distance = math.sqrt((x - Sitesx[i])^2 + (y - Sitesy[i])^2)
-- check to see if this distance is the same (within deviation) as previously determined smallest distance
checkDiff = math.sqrt((distance-smallest)^2)
if checkDiff < Deviation then -- if the difference is smaller than the allowed border width, the pixel is in a border
border = 1
else
border = 0
end
if distance < smallest then -- if the distance is smaller than any previously found distance, use it as the new smallest
smallest = distance
p.R = CellColorRList[i]
p.G = CellColorGList[i]
p.B = CellColorBList[i]
p.A = CellColorAList[i]
end
if distance < SiteSizeList[i] and ShowSites == 1 then -- provide an option to turn this off
point = 1
p.R = SiteColorRList[i] * (1 - distance/SiteSizeList[i]) + p.R * (distance/SiteSizeList[i])
p.G = SiteColorGList[i] * (1 - distance/SiteSizeList[i]) + p.G * (distance/SiteSizeList[i])
p.B = SiteColorBList[i] * (1 - distance/SiteSizeList[i]) + p.B * (distance/SiteSizeList[i])
p.A = SiteColorAList[i] * (1 - distance/SiteSizeList[i]) + p.A * (distance/SiteSizeList[i])
end
if border == 1 and ShowBorders == 1 then
p.R = p.R * (checkDiff/Deviation) + BorderColorRList[i] * (1 - checkDiff/Deviation)
p.G = p.G * (checkDiff/Deviation) + BorderColorGList[i] * (1 - checkDiff/Deviation)
p.B = p.B * (checkDiff/Deviation) + BorderColorBList[i] * (1 - checkDiff/Deviation)
p.A = p.A * (checkDiff/Deviation) + BorderColorAList[i] * (1 - checkDiff/Deviation)
end
end -- end of test for Sitesx
end -- end of main loop
return p
end) -- end of MultiProcessPixels
Once again, we find the distance from the current pixel to each site, but this time we keep track of the smallest such distance and also compare the distance to each other site to this distance. If the difference between the two distances is less than the Deviation variable, which is equal to border width, the pixel is considered to be within a border, and a flag indicating such is set.
The pixel initially gets a color corresponding to the cell it’s in, which is determined by whatever site is closest (i).
If the pixel is in a border and the user has Show Borders checked in the control panel, the pixel is overwritten with the border color. Unlike the prototype Poisson-only version of the fuse, this routine does a full-color assignment. I had some trouble with aliasing, so this makes a blurred border region in the same way that the site-coloring version made a blurred point. The border pixel’s color is a weighted average (Linear Interpolation, or LERP) of the cell color and the border color. The distance from the true geometric border determines the weight. (As opposed to the visible raster border, which is only an approximation.)
Parting Words
There are certainly improvements to be made. Among them are animation—I’ve devised a random walk algorithm that works for a single point, but I fear it will be prohibitively expensive as the number of sites increases. If I can find a way to make the sites list persistent instead of having to regenerate it on every frame, I think I can make that work. There is also some guidance from Íñigo Quílez on fixing the borders so they don’t splay out as they get further from the center. I will try to implement that at the same time that I attempt to make an OpenCL version of the Fuse. So far, my ventures into OpenCL have been nothing but frustrating. That will probably also be a good opportunity to look into better anti-aliasing options.
There are some other segmentation algorithms I’d like to try. I have a pretty good idea of how to calculate the Manhattan version, and I’ve read references to something called Minkowski, but I haven’t yet seen an example of what that means. There are also several more site distribution algorithms to examine.
The ability to allow cells to inherit color from an input image, sampling either the pixel under the generating site or from under the geometric center of the cell, would be an important advancement. There is also the possibility of allowing the user to designate positions for some or all of the sites. And publishing the site coordinates would give other tools access to information about the diagram. There’s so much potential, and I haven’t the foggiest how to do any of it!
The current version of the MT_Voronoi fuse is here.