This is the fourth article in a series on OpenCL Fuse development for Blackmagic Fusion. I am attempting to convert the lessons from the Book of Shaders into working Fuses, learning a bit about programming and parallel processing as I go.
BoS devotes a chapter to “Shaping Functions,” which are methods of modifying a gradient. Beginning with a simple linear interpolation (LERP), I’ll build up several one-dimensional functions and experiment a little bit more with the control panel.
Since the Fuse is starting to turn into something interactive and fun to play with, I’m going to go ahead and provide the complete code:
That will also make it a little easier to follow along, since this article is over 2000 words long, and I don’t want to make it even longer and drier by posting 600 lines of Lua.
The NotifyChanged() Function
Each of the modules I have built so far have different requirements for input. Up until now, I’ve left everything in same window, and everything has been exposed all the time. As things become more complex, I want to simplify the user experience, exposing only the controls that are applicable to the mode at hand. This feature requires another function called NotifyChanged() and some additional parameters on the controls.
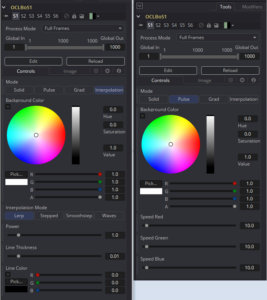
For any control with the parameter INP_DoNotifyChanged = true, Fusion will call the NotifyChanged() function whenever that control’s value is altered. This, in combination with the parameter IC_Visible allows you to create a dynamic control panel. In this case, I have hidden the Speed sliders when Solid is selected and all of the controls with Grad is selected. Since the default mode when the tool is created is Solid, I have added IC_Visible = true to InMode, inRed, inGreen, and inBlue. All of the other controls get IC_Visible = false. Now, when the tool is added to the Flow, only the mode selection buttons and the Background Color controls are visible. The other controls still exist, but they’re not displayed.
To toggle the controls’ visibility based on which mode the tool is in, I add this function:
function NotifyChanged(inp, param, time)
if inp ~= nil and param ~= nil then
if inp == InMode then
if param.Value == 0 then
inRed:SetAttrs({IC_Visible = true})
inGreen:SetAttrs({IC_Visible = true})
inBlue:SetAttrs({IC_Visible = true})
inAlpha:SetAttrs({IC_Visible = true})
inSpeedR:SetAttrs({IC_Visible = false})
inSpeedG:SetAttrs({IC_Visible = false})
inSpeedB:SetAttrs({IC_Visible = false})
elseif param.Value == 1 then
inRed:SetAttrs({IC_Visible = true})
inGreen:SetAttrs({IC_Visible = true})
inBlue:SetAttrs({IC_Visible = true})
inAlpha:SetAttrs({IC_Visible = true})
inSpeedR:SetAttrs({IC_Visible = true})
inSpeedG:SetAttrs({IC_Visible = true})
inSpeedB:SetAttrs({IC_Visible = true})
elseif param.Value == 2 then
inRed:SetAttrs({IC_Visible = false})
inGreen:SetAttrs({IC_Visible = false})
inBlue:SetAttrs({IC_Visible = false})
inAlpha:SetAttrs({IC_Visible = false})
inSpeedR:SetAttrs({IC_Visible = false})
inSpeedG:SetAttrs({IC_Visible = false})
inSpeedB:SetAttrs({IC_Visible = false})
else
inRed:SetAttrs({IC_Visible = false})
inGreen:SetAttrs({IC_Visible = false})
inBlue:SetAttrs({IC_Visible = false})
inAlpha:SetAttrs({IC_Visible = false})
inSpeedR:SetAttrs({IC_Visible = false})
inSpeedG:SetAttrs({IC_Visible = false})
inSpeedB:SetAttrs({IC_Visible = false})
end
end
end
end
NotifyChanged() takes three arguments: inp is the control that caused Fusion to call the function, param is the specific parameter that was modified, and time is the current frame. The function opens with some tests to make sure something actually did change—as long as inp and param have values, stuff will happen. Next, it checks for the actual value of param and sets IC_Visible on each control appropriately. The end result is that when you select a different button in the MultiButton control, the control panel changes to display only those sliders that are appropriate for the new mode.
There are some other possibilities for NotifyChanged(), and if I wind up using one, I’ll document it at that time. For now, I’ll just recommend taking a look at some existing Fuses for more ideas about how to use it. If I recall correctly, the TimeMachine Modifier Fuse has something going on in there.
Linear Interpolation and the Gamma Function
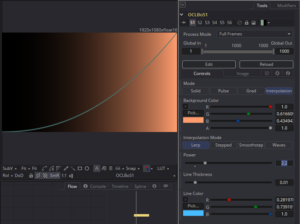The simplest of shaping functions is a simple Linear Interpolation, or LERP. This method assigns a direct, linear relationship between the value of a pixel and some other quality. In this case, we’ll assign it to the x position: RGB = brightness * x. We’ve actually already seen this in the gradient mode from the previous article. In this mode, I’m going to add a graph line that plots the brightness on y and also add a power control. (Power is the inverse of gamma. Most tools will use “gamma” to mean either, but I wanted to be sure I remembered exactly what I was doing mathematically.) Technically, adding the power function means that this mode is misnamed. It’s no longer linear, but I don’t feel like going back to correct it since this is purely for my own education.
The power calculation is simple:
float y = native_powr(st.x, power);
As before, st.x is the normalized x position coordinate (recall that we divided the actual pixel coordinate by the overall resolution to get a normalized value). The second argument, power, is driven by a control I added to the Fuse. You can use just powr() to calculate the power function, but native_powr() designates a device driver-specific implementation that is usually faster. The level of accuracy in this function is impossible to determine since it may be different for every device driver. That’s really not a problem for this application, so I’ll take the extra speed.
So the normalized x coordinate is raised to the power of a user-defined exponent, and the result is stored in the variable y. That is all that is necessary to create a gradient with an interactive gamma curve. Since this is a one-dimensional function, we can use the height of the image to help visualize the function. BoS implements a graph line that plots the brightness using the smoothstep() function. We’ll explore smoothstep() in a bit more detail in a little bit. For now, I’ll just add a bit more code that creates and renders the line.
First, since we’re going to use this line plot in several other kernels, we’ll make it a separate function:
float plot(float2 st, float ptc, float sz)
{
return smoothstep( pct - sz, pct, st.y ) - smoothstep( pct, pct+sz, st.y );
}
I’d like to draw your attention to the lack of the kernel descriptor in that function declaration. This function is meant to be called as a subroutine in other functions—it will never be invoked by the OCL Manager. This is an important distinction, as a kernel can not be called by another kernel, and a non-kernel function can not be run outside of a normal kernel operation.
As I said, we’ll get into what smoothstep() actually does later. For now, suffice to say that it takes in the normalized coordinate of the pixel to be rendered, the brightness multiplier value calculated by the power function (y), and the desired width of the line. If the pixel’s y position is within a certain distance of its brightness, as determined by the sz value, a brightness value is returned to the kernel. Here’s the function call:
float pct = plot(st, y, sz);
The argument sz is another new variable with a knob in the Fuse’s control panel. Now we have the brightness of the pixel, as determined by its position and the exponent, and an additional brightness value stored in pct. I’ll combine all of this information with some user-provided color values to determine the actual color of the pixel to be returned to the Fuse.
float3 color = (float3)(y);
color = (1.0f-pct) * color + pct * linecol;
float4 outcol = (float4)(color, 1.0) * col;
I want the Alpha to be constant across the image, so I’m using only a float3 to hold the calculated brightness multiplier. The color is then modified by the value for the line. This is actually an additive Merge operation (see, eventually, the appendix of my book that deals with Merges and Blending Modes), with pct standing in for the alpha of the line. Where pct is 1, the color is darkened, making a “hole” for the line. Where pct is 0, linecol is also reduced to 0, leaving the color intact. The result of this operation is the new value for color.
The final line multiplies our color value by the user-selected color and assigns it to the output variable. I could possibly have chosen less confusing variable names, but I was following the BoS example, which didn’t deal with user-supplied values.
The other shaping functions will use this same method of generating and combining the line with the final image.
Stepped Interpolation
I will ultimately have four sub-modes in this Interpolation mode, so it’s time to add another Multi-Button. This one works just like the previous button, except that it’s hidden by default and only revealed when the Interpolation Mode is chosen. I have alluded to some more control that I have added as well: Line size, line color, and power. To those, add a Threshold, min and max values, and frequency. I’ve given each of these a slider and visibility controls related to whichever mode they’re intended to operate in. They all get Line Thickness and Line Color. For the Stepped Interpolation mode, I need to add only Threshold. Perhaps eventually I’ll also add a Number control to determine the number of steps it creates.
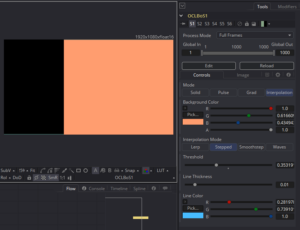A Stepped interpolation “jumps” from one value to another without covering any of the intermediate values. It’s a little difficult to see, but the plot line is still there. It’s pegged to the very bottom and top of the image.
In this mode, we replace the native_powr() function with step().
float y = step(threshold, st.x);
Once again, y holds a brightness multiplier that will be applied to the user-supplied Background Color. In this function, if st.x exceeds the threshold value, the output of step() is 1. If not, it’s 0. Very simple. Everything else in this kernel is identical to the lerp kernel.
Smoothstep
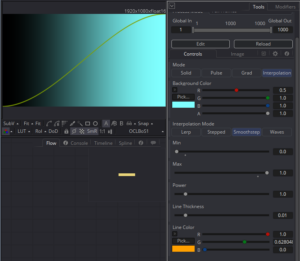As promised, we come to the smoothstep() function. This one gets two additional arguments: min and max. After Effects users are probably familiar with the Easy Ease keyframe setting that smooths out animation bumps. Simplistically, that’s a smoothstep. It takes three arguments: A lower threshold, an upper threshold, and a value. It then returns 0 if the value is below the lower threshold or 1 if the value is above the upper threshold. If the value is somewhere between those two limits, the return value is selected by smoothly interpolating between the limits using a sort of S-shaped curve, as seen in the image above. By choking the Min and Max, the transition area can be compressed, but the smoothstep() still creates a gradual transition between the two, at least until Min and Max are equal, in which case it becomes identical to the Stepped mode.
Recall that I am using smoothstep() to create the line that graphs these functions. This smooth interpolation is what causes the line to be blurry—it’s fading smoothly into the background color.
I could just leave the Smoothstep at that, but being an inveterate tinkerer, I decided to put the power function in there, too. Once again, only one line needs to be changed:
float y = native_powr(smoothstep(min, max, st.x), power);
This is an example of using the output of one function to create an argument for another function. Smoothstep() outputs a value to be used as an argument to native_powr(), which returns its own result to y.
Waves
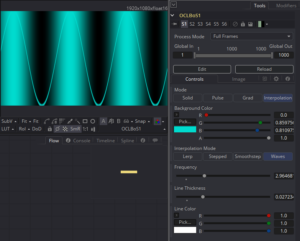This last mode isn’t really an interpolation mode (much like my lerp mode isn’t necessarily linear). But it was part of the same chapter in BoS, so I lumped it together with the rest. This one uses a sin() function to determine the brightness of the pixels by their x-coordinate.
It takes a Frequency argument that controls how many iterations of the wave are created. It also uses a special built in constant: M_PI, which holds the value of π (3.14159265…). OpenCL’s trigonometry functions operate in radians, so having easy access to π is useful. The basic formula for the sine wave is sin(x*2*π*frequency). We multiply by two because π is actually only half a circle. To get all the way back around to 0, we need to double it. This expression will return negative values, so there’s a little bit of additional jiggery-pokery to force it into a normalized range:
float y = 0.5 * (sin(st.x*M_PI*2*frequency) + 1);
Normally, sin() will return values ranging from -1 to 1. Adding 1 creates a brightness shift, bringing the range to 0 to 2. Then dividing by to normalizes it, placing all of the colors into the viewable range.
More Functions
The Book of Shaders recommends coding up a few more shaping functions and provides references to several other websites and articles for inspiration. I’ll probably do that at some point, but this article is long enough already. You may see them appear in future versions of the Fuse(s), and if I need one for a particular purpose, I will be sure to detail it at that time.
In the next article, I’ll start to apply all of this foundational information to the creation of shapes. The Book of Shaders has a chapter on color next. I assume that most Fusion users are already fairly adept with representing color with numbers and choosing a pleasing palette, so I’m going to skip that one. It didn’t have very much interesting code in it, anyway.
<< Previous Article – Position and Time
Next Article — Shapes >>
